Sistemas de numeração: Decimal, Binário e Hexadecimal.
Na semana passada um leitor lançou-me o desafio para escrever uns artigos sobre os sistema de representação numérica (sistemas de numeração). Nos sistemas digitais/computação é frequente recorrer-se a diferentes sistemas de numeração para proceder à representação da informação digital. O sistema de numeração decimal (ou na base 10), que usa dez algarismos é sem duvida o sistema mais utilizado por seres humanos e o sistema binário é o mais frequente no mundo da computação, apenas são utilizados os valores 0 e 1 (pois facilita a representação de tensões), no entanto, existem outros como o sistema de numeração Octal, Hexadecimal, entre outros. Para iniciar esta rubrica, hoje vamos conhecer as principais diferenças entre os sistemas de numeração Decimal, Binário, Octal e Hexadecimal.
A conversão entre sistemas numéricos é realizada com base em regras. A quantidade de algarismos disponíveis num sistema de numeração designa-se de base, sendo que a representação numérica mais utilizada é a notação posicional (valor atribuído a um símbolo dependente da posição em que este se encontra, num conjunto de símbolos).
Alguns sistemas de numeração
- Decimal (base 10)
- Binário (base 2)
- Hexadecimal (base 16)
Sistemas Decimal
Tal como referido, o sistema Decimal é o sistema mais utilizado pelos seres humanos, normalmente para indicar quantidades, e é constituído por dez algarismos: 0,1,2,3,4,5,6,7,8,9.

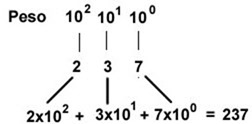
No sistema decimal cada algarismo tem um valor posicional, ou seja, cada algarismo tem um peso de acordo com a sua posição na representação do valor.
Sistema Binário
O sistema binário é o sistema mais utilizado por máquinas, uma vez que os sistemas digitais trabalham internamente com dois estados (ligado/desligado, verdadeiro/falso, aberto/fechado). O sistema binário utiliza os símbolos: 0, 1, sendo cada símbolo designado por bit (binary digit).

Sistema Hexadecimal
Sistema de numeração muito utilizado na programação de microprocessadores, especialmente nos equipamentos de estudo e sistemas de desenvolvimento. Utiliza os símbolos: 0,1,2,3,4,5,6,7,8,9 do sistema decimal e as letras A,B,C,D,E,F. Equivalências:A=10,B=11,C=12,D=13,E=14eF=15.
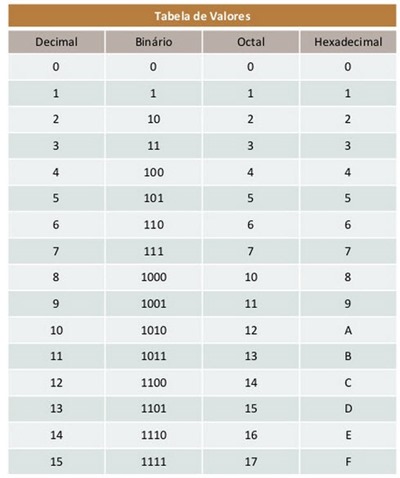
Tabela de conversão de bases
Num próximo artigo iremos ensinar a proceder à conversão entre sistemas de numeração. Desde já convidamos os leitores que estejam interessados em colaborar com esta rubrica, que enviem um e-mail para o nosso endereço geral.
alguns tipos de conversons.
Conversão de binário para decimal
Como já vimos no artigo anterior, o sistema binário só possui 2 algarismos. Cada posição tem um peso de uma potência de 2 (base do sistema binário). Sendo assim, para se converter um número de binário para decimal, deve-se multiplicar cada bit pela potência de sua posição e somar os resultados.
Por exemplo, a conversão do número 10112 para decimal é feita da seguinte forma:
Binário
|
1
|
0
|
1
|
1
|
Valor da posição
|
1 X 23
|
0 X 22
|
1 X 21
|
1 X 20
|
8
|
0
|
2
|
1
| |
Resultado
|
8+0+2 + 1 = 11 decimal
| |||
Conversão de decimal para binário
Para realizar a conversão de decimal para binário, realiza-se a divisão sucessiva por 2 (base do sistema binário). O resultado da conversão será dado pelo último quociente (MSB) e o agrupamento dos restos de divisão será o número binário.
Por exemplo, vamos converter o número 45 em binário:
A leitura do resultado é feita do último quociente para o primeiro resto. Sendo assim, o resultado da conversão do número 45 para binário é: 1011012.
Conversão de hexadecimal para decimal
A conversão de hexadecimal para decimal segue o mesmo princípio apresentado para o sistema binário. Multiplica-se cada dígito pela potência de 16 relativa à posição e somam-se os resultados:
Por exemplo, a conversão do número 12C16 para decimal:
Hexadecimal
|
1
|
2
|
C
|
Valor da posição
|
1 x 162
|
2 X 161
|
12 X 160
|
256
|
32
|
12
| |
Resultado
|
256 + 32 + 12 =300 decimal
| ||
Conversão de decimal para hexadecimal
Para converter um número decimal em hexadecimal realiza-se a divisão sucessiva por 16 (base do sistema hexadecimal), semelhante à conversão de decimal para binário.
Por exemplo, vamos converter o número 438 em hexadecimal:
O resultado é lido da direita para a esquerda a partir do último quociente. Assim. 438 é igual a 1B616.
Note que o resto da segunda divisão foi o número 11, que corresponde ao número B em Hexadecimal.




Nenhum comentário:
Postar um comentário